Franz Lemmermeyer

Topics in Algebraic Geometry: Elliptic Curves

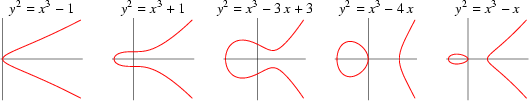
Comments

John Baez, a well known mathematical physicist, writes an enlightening weekly column about what is happening in his area. Here's week 201.

Schedule

 
    Monday     11:40 - 12:30, SBZ-11
    Wednesday  10:40 - 12:30, seminar room

You will be graded on take home exams and homework.

Content and Preliminaries

From the quiz I gather that all of you have some background in complex analysis, and that the majority is interested in abelian varieties. As for the other topics: I will review some of them briefly in class. Of course I will get nowhere if I do everything from scratch, so here's my suggestion: I will discuss affine and projective spaces, the snake lemma, p-adic numbers, and eventually a simple case of Riemann-Roch in Algebraic Geometry; you don't have to attend, but probably should read the notes. In this class, I will explain these concepts more briefly, but maybe also more informally.
You will also need a little bit of Galois theory; let me advertise my own seminar on Galois theory this semester: if more than one student is interested, we'll do it. It will also give you a short introduction to algebraic number theory. Email me if you're interested.

Books

J. Silverman, J. Tate: Rational points on elliptic curves
The most elementary introduction.

J.W.S. Cassels: Elliptic Curves.
From Amazon.com:

     Customers interested in LMSST: 24 Lectures on Elliptic Curves
     may also be interested in:
     Curves For Women
     Franchise Opportunity for Ladies Only 30 Minute Workout Club.

Actually it's quite a good book, even for men (Cassels' book, I mean).

L. Washington: Elliptic Curves
This one has just appeared. It is very elementary.
A. Knapp: Elliptic Curves
Gives a nice introduction to the analytic aspects
J. Silverman: Arithmetic of Elliptic Curves
The standard reference
Husemöller: Elliptic Curves
There will be a new edition in 2004

Topics

Group law on conics and elliptic curves
Review of p-adic numbers
Nagell-Lutz: torsion points and formal group laws
Heights
Mordell-Weil: 2-descent
Galois Cohomology
Selmer and Tate-Shafarevich groups
Function fields and divisors
The group law via divisors
Weil pairing
Modular Forms
Advanced Topics (Taniyama-Shimura, complex multiplication, Eichler-Shimura, Fermat's Last Theorem, abelian varieties, ...)

Homework Problems

macros required for the tex files.
Due Feb 23: problems (tex file); solutions.
Due March 03: problems (tex file); solutions.
Due March 17: problems (tex file);
Due at the end of March: Midterm 1 problems (tex file); solutions.
Due April 19: problems (tex file); (hints).
Midterm 2 problems (tex file);
Final problems

Software

Here's a windows executable of pari. If you type in ?, you'll get a list of chapters; ?4 lists e.g. the number theoretical functions, and ?gcd tells you what gcd does. You can find a more detailed manual at the pari homepage in Bordeaux.
John Voight gives a description of how to use pari (and other programs) for computing with elliptic curves.

Schedule

We 11.02.04 Historical Remarks; Fermat's Last Theorem for exponent 4. Lecture 1
Additional Material: here's a timeline for Fermat's Last Theorem.
Fr 13.02.04 Overview: Arithmetic of Conics and Cubics. Lecture 2
Additional Material: I shortly mentioned p-adic numbers and Hasse's Local-Global Principle. Capi Corrales Rodriganez wrote a very gentle introduction to p-adic numbers, and Catherine Goldstein gave a similarly down-to-earth introduction to elliptic curves from the p-adic point of view. We'll later return to these topics and discuss them in more detail (and with proofs!).
Mo 16.02.04 Overview: L-series, Birch-Swinnerton-Dyer conjecture. Lecture 3
Here's Wiles' ``Clay'' article on the Birch and Swinnerton-Dyer conjecture.
We 18.02.04 Projective Closure of affine curves. Lecture 4
Fr 20.02.04 Lecture 5: Singular points
Mo 23.02.04 Lecture 6: algebraic groups; group laws on lines and conics
We 25.02.04 Lecture 7: Tate's formulas; Group Laws on Cubics. Here's Tate's Inventiones article
Mo 01.03.04 no class; moved to 20.02.04
We 03.03.04 (10:40 SAZ02) Lecture 8: conics over finite fields; Pollard's p-1 method. record factors found by p-1;
Mo 08.03.04 (11:40 SAZ02) Lecture 9: factorization algorithms; at this page you can watch numbers getting factored using ECM.
We 10.03.04 Lecture 10: The Hasse bound (Manin's Proof)
Mo 15.03.04 Lecture 11: Manin's Proof Part II
We 17.03.04 Lecture 12: p-adic numbers. For a couple of introductory essays, see this page.
Mo 22.03.04 (10:40) Lecture 13: Hensel's Lemma; conics over Z_p
We 24.03.04 No class; moved to 20.02.04 and 22.03.04
Mo 29.03.04 Lecture 14: Reduction modulo p.
We 31.03.04 Lecture 15: Elliptic curves over Local Fields
Mo 05.04.04 Lecture 16: Theorem of Nagell-Lutz on torsion points;
We 07.04.04 Lecture 17: Elliptic curves over the complex numbers. Here's an article by Schappacher and Schoof on the life and the work of Beppo Levi. Here's a nice little web page on torsion points
Mo 12.04.04 Lecture 18: families of elliptic curves with cyclic torsion groups of order up to 10; nonexistence of torsion groups of order 11 over the rationals. Here's the article by Billing and Mahler; Ogg's article on the nonexistence of rational torsion points of order 17; and finally the article by Mazur and Tate on the nonexistence of rational torsion points of order 13, just to show you that even this special case is highly nontrivial.
We 14.04.04 Lecture 19: Modular Curves, Isogenies, Mazur's Proof. Here's a nice article by Lenstra and de Smit on connections between one of Escher's drawings and a certain elliptic curve.
Mo 19.04.04 (10:40) Lecture 20: Weak Mordell-Weil: the finiteness of E(Q)/2E(Q)
We 21.04.04 No class; one hour moved to 19.04, the other one to some location t.b.a.
Mo 26.04.04 Lecture 21: Heights
We 28.04.04 Lecture 22: Theorem of Mordell-Weil
Mo 03.05.04 Lecture 23: 2-descent via isogenies.
We 05.05.04 Lecture 24: exact sequences, Tate's formulas; here's the intro to It's my turn
Mo 10.05.04 Lecture 25: First steps in Galois cohomology
We 12.05.04 Lecture 25: Selmer and Tate-Shafarevich groups; 15.30: Proof of Fermat's Last Theorem
payback time: Mesut has the evaluation sheets; please fill them out if you find the time.
Mo 17.05.04. No class (I will be here); moved to 12.05.04
Here I will list a few files containing material we could not cover. More to follow.
1. Here's an explanation of the general 2-descent on elliptic curves.
2. A few incoherent remarks about Wiles' proof of FLT.

Here are Nigel Boston's notes on Wiles' proof of Fermat's Last Theorem. And here is a page with several low-brow introductions to the proof, along with the original articles.