These are some explanatory notes to
my
manuscript with the same title.
Methods of quantum computing derive their benefit from the inherent property of parallelism of quantum operations on a superposition of states. That is to say, if one is to perform the operation U on the superposed state*
| n1 > + | n2 > + | n3 > + . . . , (1)then one obtains the new state*
U | n1 > + U | n2 > + U | n3 > + . . . . (2)Methods of quantum computing associate possible outcomes to the states | ni > and carry out unitary transformations on these states, until a final state which represents the solution to the problem at hand is obtained. A measurement is then carried on this final state , which yields only one (or a particular class of) these final states. This measurement then yields information about the solution. Depending on the algorithm, this information may be definite, or may be probabilistic, in which case the computation (i.e., the transformation plus measurement) may need to be repeated a number of times to obtain a final result.
The microscopic interactions that drive quantum systems are linear, and the transformations U which act upon superposed states must be unitary. Although this limitation still allows for a rich class of problems which may be attacked through quantum computation, it is interesting to consider what other type of problems would lend themselves to such an analysis if nonlinear operations on states were also permitted.
The states | ni > are usually classified in terms of the binary decomposition of the number ni which labels the quantum states. The binary bits are then referred to as "qubits". Since the unitary transformations U map the quantum states into linear combinations of such states, they may be thought as operating on the qubits. Consider for example, the unitary transformation which carries out the following set of transformations on two-qubit states:
|00> -> |00> |01> -> |01> |10> -> |11> (3) |11> -> |10> .The transformation is unitary, and it can be shown to be related to the unitary matrix
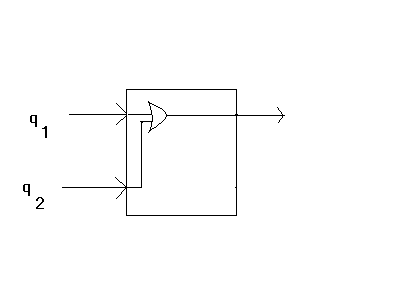
1 0 0 0 0 1 0 0 0 0 0 1 (4) 0 0 1 0acting on the 4 basis states in the order given on the left hand side of the relations in (3). Another way of describing this operation is through the operation of a "quantum-gate" which this transformation represents. Note that in all of the transformations in (3), the first qubit is unchanged, and the second qubit is changed if the first one is equal to 1. This results in a second qubit which is 0 if the two input qubits are equal to one another, and 1 otherwise. The state of this second qubit is equivalent to the classical XOR operation of the two input qubits. It is for this reason that the transformation in (3) is also referred to as a quantum XOR operation and is shown by this operational diagram:
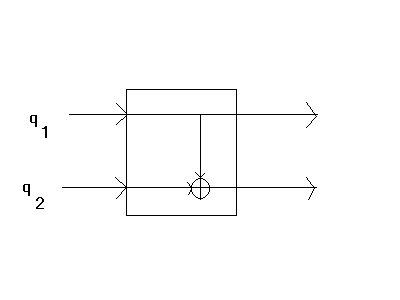
The transformation in which the second qubit is transformed into the classical OR of the two input qubits
|00> -> |00> |01> -> |01> |10> -> |11> (5) |11> -> |11>is not unitary, and would not normally be allowed in the construction of a quantum computing algorithm. The reason for this is that there is no fundamental physical process through which such a transformation of the states would be possible. However, we know from everyday life that not all things operate linearly (including all of the classical computers which have lots of OR gates built into them), although in principle all of these operations are intrinsically built upon microscopic quantum mechanical interactions. A well known statement of this fundamental problem is the case of the "Schrodinger's cat", in which the well being of a macroscopic object (the cat) is questioned, whether it can be in a superposition of the "alive" and "dead" states. (The original discussion has the cat in a superposition of states coupled to a single qubit, but it is a straightforward exercise to extend it to any logical function of a number of qubits.) A through discussion of this problem cannot be provided here, and the interested reader may refer to this link and the references therein. It is generally considered that the disturbing part of this perspective is that the cat is a very large object, in interaction with a lot of other states which destroys the delicate coherence in the superposition of the states that it is composed of.
The question remains however, if it is possible to construct relatively
small systems, with sufficient isolation from the external events, but also with
sufficient internal complication to yield a nonlinear development of
the quantum state. If such a system could be constructed, one could
implement a nonlinear quantum gate which corresponds to a transformation
as given in (3).

My work ( M.C.Yalabik, Mod. Phys. Lett. B 20, 1099 (2006)) proposes that such a transformation would be possible if the qubits were to develop in time according to the nonlinear Schrodinger equation. (Also see Yu Shi, J. Mod. Phys. B15, 3007 (2001).) This equation was derived through an approximation to describe (among other things) the time development of the order parameter in a Bose-Einstein condensate. Since it involves an approximation (as it must, since the exact time development of the full system is expected to be linear), and because it represents the time development of not a single quantum degree of freedom, but of a collective state, it is not immediately apparent that Bose-Einstein condensates could be used in a physical implementation of this gate. Part of the problem may be considered to be technical, admittedly one would have to show how the input and the output qubits of such systems would be connected to the nonlinear system for the method to be applicable. A deeper question is whether the quantity which is modelled by the nonlinear equation still has the required quantum properties such as entaglement, superposition, interference, probabilistic interpretation, etc. There seems to be some experimental and theoretical evidence that this may indeed be so.
How would such nonlinear quantum gates affect the class of problems that can be attacked by quantum computation? (Also see D.S.Abrams and S.Lloyd, Phys. Rev. Lett. 81, 3992 (1998). [A number of discussions on the Internet by Lou Pagnucco on this subject predate formal publications.]) One set of such problems involves the step by step elimination of a set of choices among the available possibilities in the search of an optimal (in some sense) case. Consider for example the search for an optimal move in the course of a game. One could search through all possible future plays, eliminating those which lead to unfavorable results through comparisons of these results. To see how this could be done, let us invent a very simple game in which players have the option of making one of two possible moves (0 or 1) alternately during the course of the game. If the game is known to reach an end after n moves, all possible ways this game could be played may be represented by all possible values n binary bits could take. To be more specific, let us specify the game a little more: Suppose that the game involves alternately picking up a number of match-sticks from a table. Each player has the option of picking up either one or two sticks at a time, and the player picking up the last set of sticks wins. It is possible to find very efficient artificial intelligence based optimal strategies for this simple problem. However, for quantum computation it is more feasible to have a brute-force approach which analyses all possible ways the game could be played, which could be extended to more complicated games.
Suppose that at some stage in the game, there are three remaining sticks on the table, and the quantum computer (Q) and the other player A (Alice?) will take turns picking them up. Denoting the action of picking a single stick up as 0 and picking up two sticks as 1, the possible ways this game could end are given by the following set of moves, assuming it is Q's turn to play next:
moves winner
------- ------
Q A Q A
0 0 0 0 A
0 0 1 Q (6)
0 1 0 Q
1 0 0 Q
1 1 A
Note that Q has a winning strategy, by playing a 0 initially, and then the
complement of A's play on her next move.
Playing a 0 after A plays a 0 would be a mistake, which would allow A to win.
In order to apply a quantum computational solution to the search for an optimal strategy, we will first list all possible values four qubits could take, and form a superposed state out of them*:
|0000> + |0001> + |0010> + . . . + |1111> (7)
We will now interpret these sequence of qubits as a sequence of moves, and
tag two more qubits to each state.
Note that this interpretation is not strictly
valid, as only the moves indicated in (6) are legal in the game. One of
the tagged qubits (L) will then indicate the "legality" of the set of moves
within the rules of the game,
while the other (W) will indicate the winning side - 0 for A and 1 for Q:
Q A Q A L W
|0 0 0 0> |1 0>
+ |0 0 0 1> |0 x>
+ |0 0 1 0> |1 1>
+ |0 0 1 1> |1 1>
+ |0 1 0 0> |1 1>
+ |0 1 0 1> |1 1>
+ |0 1 1 0> |0 x> (8)
+ |0 1 1 1> |0 x>
+ |1 0 0 0> |1 1>
+ |1 0 0 1> |1 1>
+ |1 0 1 0> |0 x>
+ |1 0 1 1> |0 x>
+ |1 1 0 0> |1 0>
+ |1 1 0 1> |1 0>
+ |1 1 1 0> |1 0>
+ |1 1 1 1> |1 0>
Qubits L and W are to be tagged to each state by the quantum computer,
operating in parallel on these states. This assumes that it is "easy" to
see if a given set of moves makes up a legal play,
and again it is "easy" to find
out which side wins if the play is indeed legal. An x state
in the table
indicates a "don't care" condition, it could be taken as 0 or 1. Note that
plays with spurious moves after a legally completed game
(such as |1100>) are still considered legal.
The two additional qubits L and W carry information about the optimality of that particular set of moves, the quantum computer will try to reach an end state with L=1 and W=1.
Information about optimality may now be transferred to a sequence of moves one less than the original one through the following mechanism. Note that (8) may be written as
Q A Q A Q L W Q L W
|0 0 0> ( |0 1 0> + |1 0 x> )
+ |0 0 1> ( |0 1 1> + |1 1 1> )
+ |0 1 0> ( |0 1 1> + |1 1 1> )
+ |0 1 1> ( |0 0 x> + |1 0 x> ) (9)
+ |1 0 0> ( |0 1 1> + |1 1 1> )
+ |1 0 1> ( |0 0 x> + |1 0 x> )
+ |1 1 0> ( |0 1 0> + |1 1 0> )
+ |1 1 1> ( |0 1 0> + |1 1 0> )
We now apply the following (nonlinear) transformation, in parallel, to
the final three qubits of this state*:
|0 L0 W0> + |1 L1 W1> -> |L' W'> (10)Where L' and W' are the qubits representing the legality and winning-side information of the "shortened" game. These qubits are defined as follows:
Following the above transformation, the superposed state corresponding to the problem now looks like
Q A Q L'W'
|0 0 0> |1 0>
+ |0 0 1> |1 1>
+ |0 1 0> |1 1>
+ |0 1 1> |0 x> (11)
+ |1 0 0> |1 1>
+ |1 0 1> |0 x>
+ |1 1 0> |1 0>
+ |1 1 1> |1 0>
Regrouping the terms as
Q A Q L'W' Q L'W'
|0 0> ( |0 1 0> + |1 1 1> )
+ |0 1> ( |0 1 1> + |1 0 x> ) (12)
+ |1 0> ( |0 1 1> + |1 0 x> )
+ |1 1> ( |0 1 0> + |1 1 0> )
and repeating the transformation at (10), one obtains
Q A L'W'
|0 0> |1 1>
+ |0 1> |1 1> (13)
+ |1 0> |1 1>
+ |1 1> |1 0>
Note that since Q is to make a choice between the |000> and
|001> moves, which determines who wins the game,
the winning side for the shortened |00> game is taken
to be Q. The opposite would be true if player A were to be making this
choice. Finally, the set of operations above may be repeated to obtain the
sequence of states
Q A L W A L W
|0> ( |0 1 1> + |1 1 1> ) (14)
+ |1> ( |0 1 1> + |1 1 0> )
and
Q L W
|0> |1 1>
+ |1> |1 0> (15)
which may be decoded to indicate "both initial moves 0 and 1 are legal,
but playing 0 leads to a winning game for Q, while playing 1 will lead
to a losing game, provided that neither player makes a mistake".
The task is then to carry out a measurement of the qubits L and W, until one obtains the result 1 for both of them. A further measurement of the remaining qubit will indicate the move corresponding to a winning strategy. (Alternatively, a different nonlinear gate operating on the triple qubits in (15) could directly provide a single qubit whose contents would indicate the winning move.) If no such measurement yields 1's for both L and W, the implication is that there is no sure winning move at this stage of the game, and best that can be hoped is that player A may make a mistake.
Note that this method could also be utilized on a classical computer, but the parallelism inherent in quantum computation would make the time necessary to compute the next optimal move (in a game with a maximum of N remaining moves) proportional to N2 in contrast to 2N for classical computation.
Cemal Yalabik

May 19th, 2003 (modified July 16th, 2003)