|

|
April 2003 |
|
Question :
Prove that
the sequence 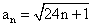 , n = 1, 2, …. contains all prime numbers except 2 and
3. , n = 1, 2, …. contains all prime numbers except 2 and
3.
Solution |
|
 |
Congratulations
|
|
 |
Jacob Tsimerman |
Toronto, Canada |
 |
Ali Yıldız |
Bilkent University, Ankara |
 |
Vlad Petrescu |
University of Florida, USA |
 |
Hung Ha Duy |
Hanoi University of Education, Vietnam |
 |
Ahmet Şensoy |
Bilkent University, Ankara |
 |
Athanasios Papaioannou |
Thessaloniki, Greece |
 |
Ünsal Atasoy |
Middle East Technical University, Ankara |
 |
Stojan Trajanovski |
High School "RJ Korcagin"
Skopje, R. Macedonia |
 |
Umut Işık |
Bilkent University, Ankara |
 |
Talat Şenocak |
Bilkent University, Ankara |
 |
Julien Santini |
Universite de Provence, France |
 |
Birol Bakay |
Bilkent University, Ankara |
 |
Zekeriya Yalçın Karataş |
Middle East Technical University, Ankara |
 |
Bruno Langlois |
Lycee Jean Rostand, Mantes, France |
 |
Özgür Ocak |
Istanbul Technical University |
 |
Erdem Özcan |
Bilkent University, Ankara |
 |
Çağrı Özçağlar |
Bilkent University, Ankara |
 |
Ali İlik , Gürel Yıldız |
Işık University, Istanbul |
 |
Şener Öztürk |
|
![]()
![]() is even, prove that at least one
is even, prove that at least one![]()